Table of Contents
ToggleWhat is regularization ?
Regularization is a technique in machine learning for preventing overfitting and improving model generalization. Some examples of regularization techniques are L1 Regularization (Lasso), L2 Regularization (Ridge), Elastic Net, Dropout, Early Stopping etc .
Note: The coefficients represent the estimated weights for each feature in the model in context of Lasso and Ridge regression.
The loss function is used to get the error rate for individual predictions whereas in the cost function the overall performance of the model is measured across the dataset. In simple terms we can say loss function is a subpart of cost function.
l1 vs l2 regression in machine learning
a) At definition level
L1 Regularization
In L1 regularization we add a penalty to the loss function which is proportional to the absolute value of the coefficients. The value of the penalty is the sum of all coefficients multiplied by a regularization parameter (lambda λ). This encourages the model to keep the coefficients small and can even eliminate some of the features making the model simpler and avoids overfitting.
Mathematical formula
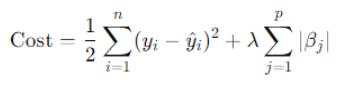
Here, formula has two parts
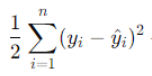
is the mean squared error term (standard linear regression part).
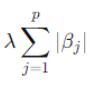
is the L1 penalty term, where |βj| (Beta) are the model coefficients and lambda (λ) is a hyperparameter that controls the strength of the regularization.
L2 Regularization
In L2 regularization we add a penalty to keep the coefficients small. The value of penalty is calculated by squaring each coefficient and then adding those squares together. The goal is to make the model simpler and prevent it from fitting too closely to the training data. This helps us to improve models performance on new data.
Mathematical Formulation:
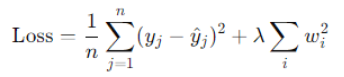
Here
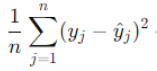
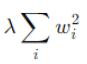
b) Primary Objective of L2 and L1 Regression
The Primary objective of l2 regression is to shrink the coefficient towards zero to reduce model complexity and multicollinearity. Whereas l1 regression shrinks coefficients towards zero for both variable reduction and model simplification.
c) Feature selection : L1 vs L2 Regression
l1 Regression actually helps to do feature selection by reducing the coefficient value to zero. l1 Regression is used in feature engineering to figure out the important columns for model training. On the other hand l2 regression does not perform feature selection. All the columns are included as the magnitude of coefficient is not zero.
d) Model Simplicity: l1 vs l2 regularization
l1 regression regularization technique produces a simpler model as compared to l2 regression technique.
e) Coefficient Behavior: l1 vs l2 regularization
Considering the coefficients in l2 regression they can reach to zero but in l1 regression they can be zero.
f) When to Use L1 vs L2 Regression
You can use the l2 when multicollinearity is present, when you want to keep all the variables, and when you have independent variables in significant numbers. l1 Regression is used when we want to do feature selection and remove lots of irrelevant features making the model simpler.
g) Sensitivity of Coefficients: L1 vs L2
In l2 regression, the sensitivity is characterized by a gradual adjustment of coefficients as the penalty parameter (lambda) varies. In contrast, l1 regression exhibits a sharp thresholding effect, where coefficients can suddenly become zero as lambda increases.
Why is regularization necessary?
- Prevents overfitting: Regularization helps in reducing the risk of overfitting by simplifying the model and preventing it from fitting the noise in the training. Overfitting model learns the noise in the data instead of the underlying patterns for prediction. Regularization reduces the chance of overfitting.
- Improve generalization: Regularization helps us make sure that the model captures the real patterns in the data rather than just memorizing particular instances. This happens by limiting model complexity. When we reduce the complexity the model generalizes well to new and unknown datasets.
- Handles Multicollinearity: When some of the feature values you use to predict an outcome are closely related to each other, it can make your predictions less reliable. Regularization helps fix this problem by adding a penalty to the model’s complexity. Ridge (L2) regularization is one way to do this. It helps by making the model less sensitive to those closely related variables. Making the model more stable and accurate predictions.
- Facilitates Feature Selection: The L1 regularization shrinks the coefficients to zero helping in selection of important features for prediction making the model accurate.
- Balancing bias and variance: Regularization creates a bias and variance tradeoff. It may increase the bias slightly making the model less accurate on training data and significantly reduce variance resulting in better performance on test data.
- Robustness to Noise: Regularized models are less sensitive to noise and outlier in the training data.
- Regularization allows us to use more complex models without the risk of overfitting.
When to use l1 regularization ?
- We use l1 regularization when we want to do feature selection.
- If we have a large dimensional data and want to automatically eliminate irrelevant features.
- When we want to make our model simple by removing some features
When to use l2 regularization ?
- We use l2 regularization when we don’t have many irrelevant features and we just want to shrink the coefficients.
- L2 regularization helps control multicollinearity or overfitting in the model.
L1 vs L2 regularization : code implementation
We are using the Iris dataset for classification tasks. It contains data about three species of iris flowers: setosa, versicolor, and virginica. We would classify the species based on following parameter: Sepal length (cm),Sepal width (cm), Petal length (cm) and
Petal width (cm).
Will perform L1 and L2 regularization on Iris dataset and check their accuracy.
L1 regularization code
from sklearn.preprocessing import normalize from sklearn.linear_model import LogisticRegression from sklearn.model_selection import train_test_split from sklearn.datasets import load_iris from sklearn.metrics import accuracy_score import numpy as npLoad dataset
data = load_iris() X = data.data y = data.targetSplit the data into training and test sets
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42)Apply L1 normalization to the features
X_train_normalized = normalize(X_train, norm='l1', axis=1) X_test_normalized = normalize(X_test, norm='l1', axis=1)Train a Logistic Regression model
model = LogisticRegression(max_iter=200) model.fit(X_train_normalized, y_train)Make predictions
y_pred = model.predict(X_test_normalized)Evaluate the model
accuracy = accuracy_score(y_test, y_pred)
print(f'Accuracy of the model after L1 normalization: {accuracy:.4f}')
Output
Accuracy of the model after L1 normalization: 0.7556
L2 regularization code
from sklearn.preprocessing import normalize from sklearn.linear_model import LogisticRegression from sklearn.model_selection import train_test_split from sklearn.datasets import load_iris from sklearn.metrics import accuracy_score import numpy as npLoad dataset
data = load_iris() X = data.data y = data.targetSplit the data into training and test sets
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42)Apply L1 normalization to the features
X_train_normalized = normalize(X_train, norm='l2', axis=1) X_test_normalized = normalize(X_test, norm='l2', axis=1)Train a Logistic Regression model
model = LogisticRegression(max_iter=200) model.fit(X_train_normalized, y_train)Make predictions
y_pred = model.predict(X_test_normalized)Evaluate the model
accuracy = accuracy_score(y_test, y_pred)
print(f'Accuracy of the model after L1 normalization: {accuracy:.4f}')
Output
Accuracy of the model after L2 normalization: 0.8667
We can conclude L2 regularization works better than L1 regularization on Iris dataset for Logistic regression model.
Conclusion
Both lasso and Ridge regression are techniques that help machine learning from overfitting on training data. Lasso regression helps in feature selection by eliminating unnecessary features. It makes the coefficients of features to zero.
Ridge regression is a better choice when we have multicollinearity. It would keep all the features but coefficients would be reduced as are needed.
Choosing to use Ridge or Lasso regression totally depends on the characteristics of the dataset and our modeling goals.
In this blog we learned Lasso vs Ridge regression in machine learning and you can also learn about the bottom layer of the decision tree.
